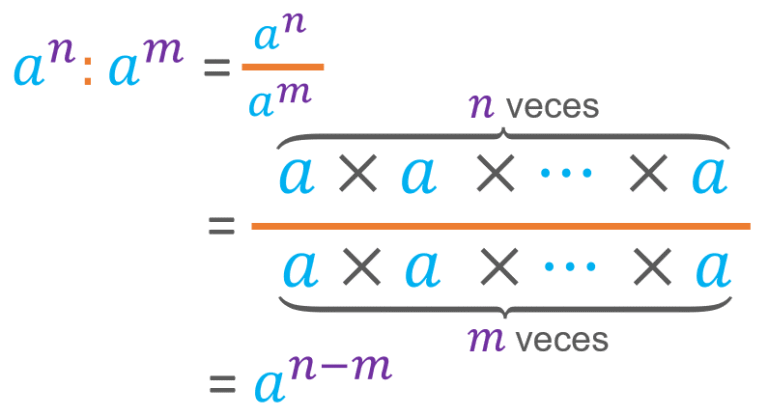Qué significa que algo elevado a cero sea igual a uno

✅ Todo número elevado a cero es uno, porque representa la identidad multiplicativa. Es un principio matemático esencial y universal.

Cuando decimos que cualquier número elevado a la potencia de cero es igual a uno, nos referimos a una de las reglas fundamentales de la aritmética y de la álgebra en matemáticas. Esto es cierto para todos los números reales, excluyendo el cero mismo, ya que 0^0 es considerado como una forma indeterminada en matemáticas. Así que, por ejemplo, 5^0 es igual a 1, al igual que 100^0 o (-7)^0.

La razón detrás de esta regla se puede entender mediante la propiedad de los exponentes. Cuando restamos exponentes en una base común, obtenemos la siguiente relación: a^m / a^m = a^(m-m) = a^0. Como cualquier número dividido por sí mismo es igual a 1 (siempre que el número no sea cero), podemos concluir que a^0 = 1.

Ejemplos para Clarificar

• 2^3 = 8: Si dividimos 2^3 y 2^3, obtenemos 1. Según la regla de los exponentes, esto se puede expresar como 2^3 / 2^3 = 2^(3-3) = 2^0, por lo que 2^0 = 1.
• 10^5 / 10^5 = 1: De la misma manera, si tomamos 10 elevado a la 5 y lo dividimos por 10 elevado a la 5, esto también da como resultado 10^0 = 1.

Aplicaciones de la Regla

Comprender que cualquier número elevado a cero es igual a uno tiene aplicaciones prácticas en diversas áreas de la matemática y ciencias. Por ejemplo, en la resolución de ecuaciones exponenciales, se utiliza esta propiedad para simplificar expresiones y solucionar problemas.

Además, este concepto es fundamental en áreas como la teoría de conjuntos, donde se utiliza en la definición de funciones y en el cálculo de límites. La base de este principio es importante para estudiantes y profesionales en campos que requieran el uso de las matemáticas.

La propiedad matemática detrás del exponente cero

La propiedad del exponente cero es un concepto fundamental en matemáticas que frecuentemente causa desconcierto entre estudiantes y aficionados. A primera vista, la afirmación de que cualquier número elevado a la potencia de cero es igual a uno puede parecer extraña, pero es perfectamente lógica al analizarla desde la perspectiva de las reglas de los exponentes.

Entendiendo la regla

Para comprender por qué se establece que x⁰ = 1, consideremos la regla de la división de exponentes. Esta regla establece que al dividir dos potencias con la misma base, se restan los exponentes:

x^a / x^b = x^a-b

Si elegimos a = 1 y b = 1, obtenemos:

x¹ / x¹ = x^1-1 = x⁰

Como cualquier número dividido por sí mismo (excepto por cero) es uno, podemos concluir:

x⁰ = 1

Ejemplos concretos

Veamos algunos ejemplos prácticos que ayudan a ilustrar esta propiedad:

• 2⁰ = 1: aquí, 2 elevado a cero es igual a uno.
• (-5)⁰ = 1: el mismo principio se aplica a números negativos.
• (1/3)⁰ = 1: incluso con fracciones, el resultado sigue siendo uno.

Casos de uso

Esta propiedad es esencial en diversas áreas de las matemáticas, incluyendo:

1. Álgebra: Simplificar expresiones algebraicas que involucran exponentes.
2. Cálculo: Ayuda en la derivación de funciones y en la evaluación de límites.
3. Estadística: En fórmulas que involucran probabilidad y combinaciones.

Un vistazo a la teoría detrás

Desde una perspectiva más profunda, la razón por la cual esta propiedad es válida también puede ser relacionada con la continuidad de las funciones exponenciales. Si consideramos la función f(x) = a^x para cualquier a > 0, observamos que:

lim_{x -> 0} a^x = a⁰ = 1

Esto refuerza la idea de que cuando acercamos x a cero, el resultado de la función se aproxima a uno.

Recomendaciones prácticas

Al trabajar con exponentes, es recomendable seguir estos consejos:

• Siempre verifica si la base es diferente de cero antes de aplicar la propiedad.
• Practica con diferentes tipos de números para afianzar la comprensión.
• Utiliza gráficos para visualizar el comportamiento de las funciones exponenciales cerca de x = 0.

Así, es posible apreciar la belleza y la lógica detrás de que cualquier número elevado a cero sea igual a uno, un concepto que, aunque simple, es fundamental en el vasto mundo de las matemáticas.

Preguntas frecuentes

¿Por qué cualquier número elevado a cero es uno?

Esto se debe a las propiedades de las potencias. Al dividir un número por sí mismo, obtenemos uno, y esto se refleja en la regla de que cualquier número elevado a cero es igual a uno.

¿Esto aplica a todos los números?

Sí, excepto en el caso del número cero. Cero elevado a cero es una indeterminación en matemáticas y no tiene un valor definido.

¿Cómo se aplica en matemáticas avanzadas?

Este concepto es fundamental en álgebra y cálculo, ya que se usa en la simplificación de expresiones y en la resolución de ecuaciones.

¿Qué pasa con los números negativos?

Los números negativos también siguen esta regla; cualquier número negativo elevado a cero es igual a uno, excepto el cero.

¿Cómo se representa esto en la notación matemática?

Se representa como a^0 = 1, donde ‘a’ es cualquier número real diferente de cero.

Puntos clave sobre elevar a cero

• Propiedad fundamental de las potencias.
• Se aplica a todos los números reales, excepto cero.
• Cero elevado a cero es indeterminado.
• Importante en álgebra y cálculo.
• Usado para simplificar expresiones matemáticas.
• Útil en la resolución de ecuaciones y funciones.

¡Nos encantaría saber tu opinión! Deja tus comentarios y no olvides revisar otros artículos en nuestra web que también te pueden interesar.